LIBRARY
Single-Phase Islanding Detection using PLL Stability

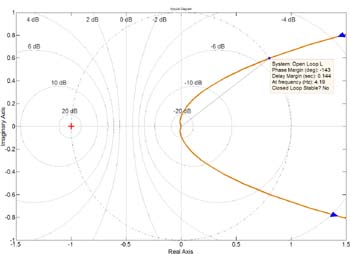
As such, the PLL system was designed to be conditionally stable, dependent upon grid dominance. It achieves this stability effect through the implementation of the PLL and corresponding Loop Filter design. With such a system, a 180° phase reversal is experienced within the PLL control loop once there is a loss of grid condition.
The Nyquist plot in Fig. 2 shows the PLL stability for a grid-disconnect condition, and how there is now an encirclement of the "-1" point, thus violating the Nyquist stability criteria and leading to an unstable frequency estimation which can easily be used as a marker for the islanding condition itself.
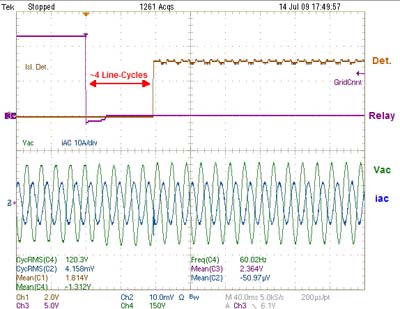
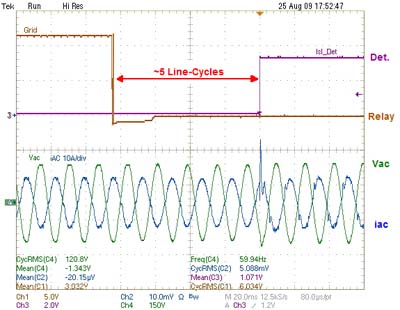
Looking to the experimental results in Fig. 3, it is seen under simple resistive loading the system can detect the loss of grid event and change over to a stand-alone, backup power mode of operation. Fig. 4 shows the results for the more complex loading of a parallel RLC with 60 Hz resonance (as required by IEEE-1547 testing specifications). There it is also seen that for the loss of grid case, the system is able to detect and change its mode of operation.