LIBRARY
Inverse Nyquist Stability Criterion for Grid-Tied Inverters
Year: 2018 | Author: Bo Wen | Paper: D4.2
Fig. 1. Polar plot of a minor loop gain
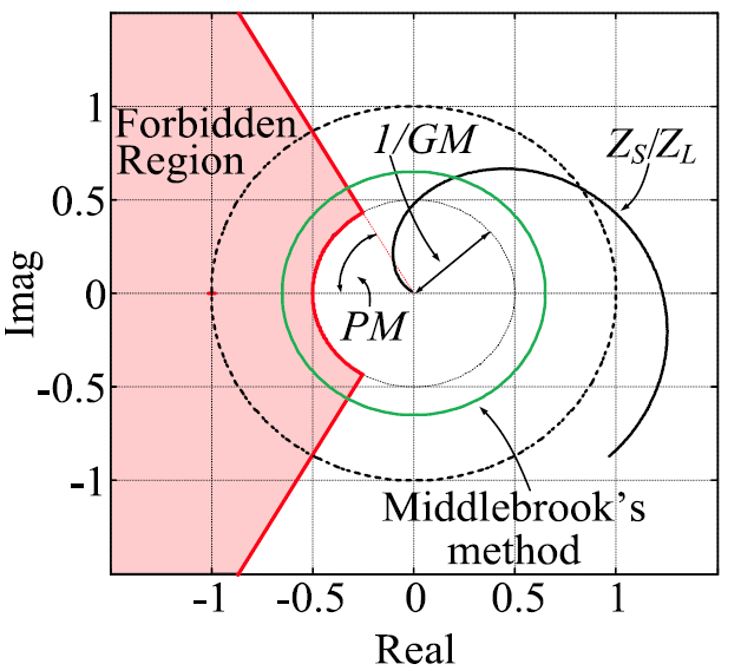
As an extension of the work done by J. Sun, this paper provides an impedance-based small-signal stability analysis of a current source system using the Thevenin equivalent circuit of the current source. The Thevenin equivalent circuit-based analysis leads to the same stability criterion proposed by J. Sun. Moreover, this paper identifies that the criterion proposed is equivalent to apply the inverse Nyquist stability criterion to the minor loop gain, where the numerator is the output impedance of the current source and the denominator is the internal impedance of the voltage source. Given the stability conditions predicted by the inverse Nyquist stability criterion are identical to the stability conditions predicted by the Nyquist stability criterion applied to the same minor loop gain, this paper demonstrates the original impedance-based stability criterion proposed by R.D. Middlebrook achieves the same stability judgment as applying the criterion from the work of J. Sun.
An impedance-based small-signal stability criterion is derived using the Thevenin representation for the current-source system. The original criterion proposed by Middlebrook can still be used for a current-source system where the poles are at the origin and the right-half-plane (RHP) must be considered. However, applying the inverse Nyquist stability criterion to the minor loop gain defined by Middlebrook is equivalent to the criterion in the work of J. Sun. For the three-phase grid-tied inverter system discussed in this paper, the current feedback controller and the phased-locked loop introduce poles to output impedance at origin and the RHP. The stability test of applying the generalized Nyquist criterion to the minor loop gain defined by the ratio of the grid impedance over the inverter impedance, or applying the generalized inverse Nyquist criterion to the minor loop gain defined by the ratio of the inverter impedance over the grid impedance, leads to an easier stability judgment. The poles at origin and RHP of the inverter output impedance can be ignored. Stability of the system is judged simply by checking whether the characteristic loci encircle the (-1, j0) point. The above analyses show that in many new applications the poles on the origin and RHP of the impedance of a component must be considered if present, since they play an important role in the impedance-based stability analysis. A three-phase experimental system validates the proposed analyses.
