LIBRARY
An Analytical Method to Calculate Winding Resistance for Planar Coil with Ferrite Plate and Litz Wire in Inductive Power Transfer
Year: 2018 | Author: Ming Lu | Paper: D5.9b
Fig. 1. (a) The cylindrical structure of an exemplary coil with a ferrite plate; (b) equivalent structure of (a) using the method of image; (c) fabricated coil of (a) for measurement.
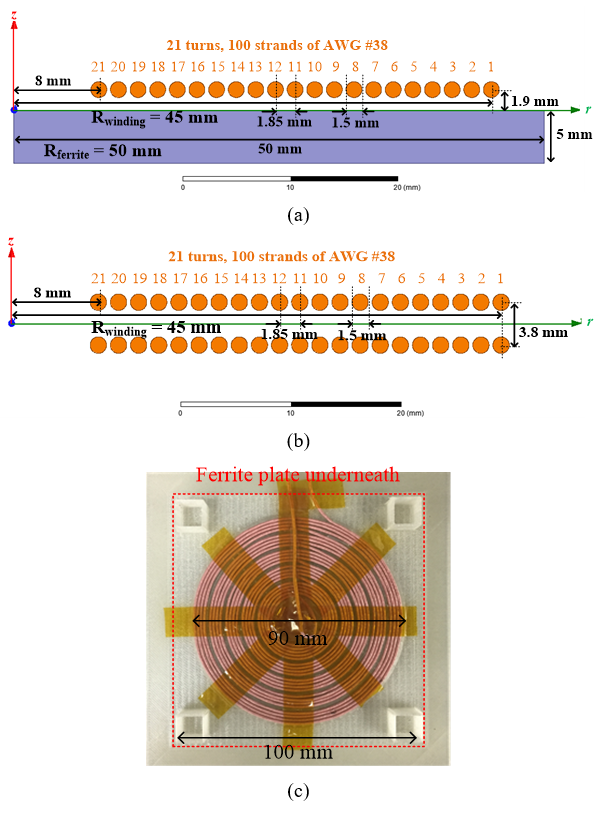
An exemplary planar coil with circular winding and a square ferrite plate was fabricated. The Litz wire was made of 100 strands of AWG #38. The dimensions of the ferrite plate were 100 mm by 100 mm by 5 mm. The winding resistance was measured with an impedance analyzer to verify the accuracy of the analytical method. The difference between the calculated and measured resistances was less than 10 percent.
Planar coil with a ferrite plate and Litz wire is used abundantly in inductive power transfer for electric vehicles. The magnetic fields across the winding turns are essential to obtain the resistance. An analytical method is described in this paper to calculate these magnetic fields. In this method, the ferrite plate is replaced by mirror turns according to the method of image. The magnetic field across each turn is decomposed to the internal field that is generated by the turn itself, and the external field that is generated by all the other turns. The internal field is calculated with Ampere's Law, and the external field is derived from Biot-Savart Law. An exemplary planar coil with 100/38 Litz wire and a square ferrite plate with dimensions of 100 mm by 100 mm by 5 mm was fabricated, and its resistance was measured with an impedance analyzer. The coil's resistance was also derived with the magnetic fields from simulation and from calculation. The calculated and simulated resistance are almost the same, and the difference between the calculation and measurement is less than 10 percent.
