RESEARCH
Gap Design for Ferrite Cores to Maximize Inductance in the Presence of Non Uniform Saturation
Year: 2014
Fig. 1. Permeability map of gapped EE core and Inductance measurement setup.
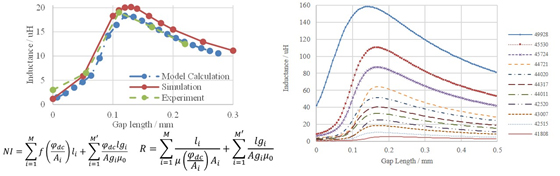
In order to assign the right permeability, the inductor should be divided into various cross-sections along the flux path. Dc operation point - φdc is then calculated using the first equation in Fig. 2(a). The total reluctance only depends on φdc if the µ-B curve of the core material is given. Maximum inductance can be derived when the first derivative of the reluctance formula equals zero. The peak position moves left with the decrease of dc current. The critical current where the peak position reaches zero is defined as the gapping current. This value can be used to determine whether a gap is necessary for an inductor. With a dc bias higher than the gapping current, the gapped core after optimization will have a larger inductance than an un-gapped core, and vice versa.
To construct an application with non-uniform permeability, the experiment of a gapped EE core with the winding around a smaller leg was carried out, as shown in Fig. 1. The calculation matches the experimental result, and the error for maximum inductance is less than 5%. Curves showing inductance versus gap length for different core dimensions were then generated to help choose a minimum-sized core to meet inductance requirement at a given dc current, as shown in Fig. 2(b).
Fig. 2. (a) Comparison of L-lgap curves from three approaches; (b) Calculated L-lgapcurves for different core sizes.
