LIBRARY
Modeling and Control of Modular Multilevel Converter
Year: 2022 | Author: Yugal Gupta | Paper: H-S6.3
Fig. 1. Decoupled equivalent circuit model of MMC
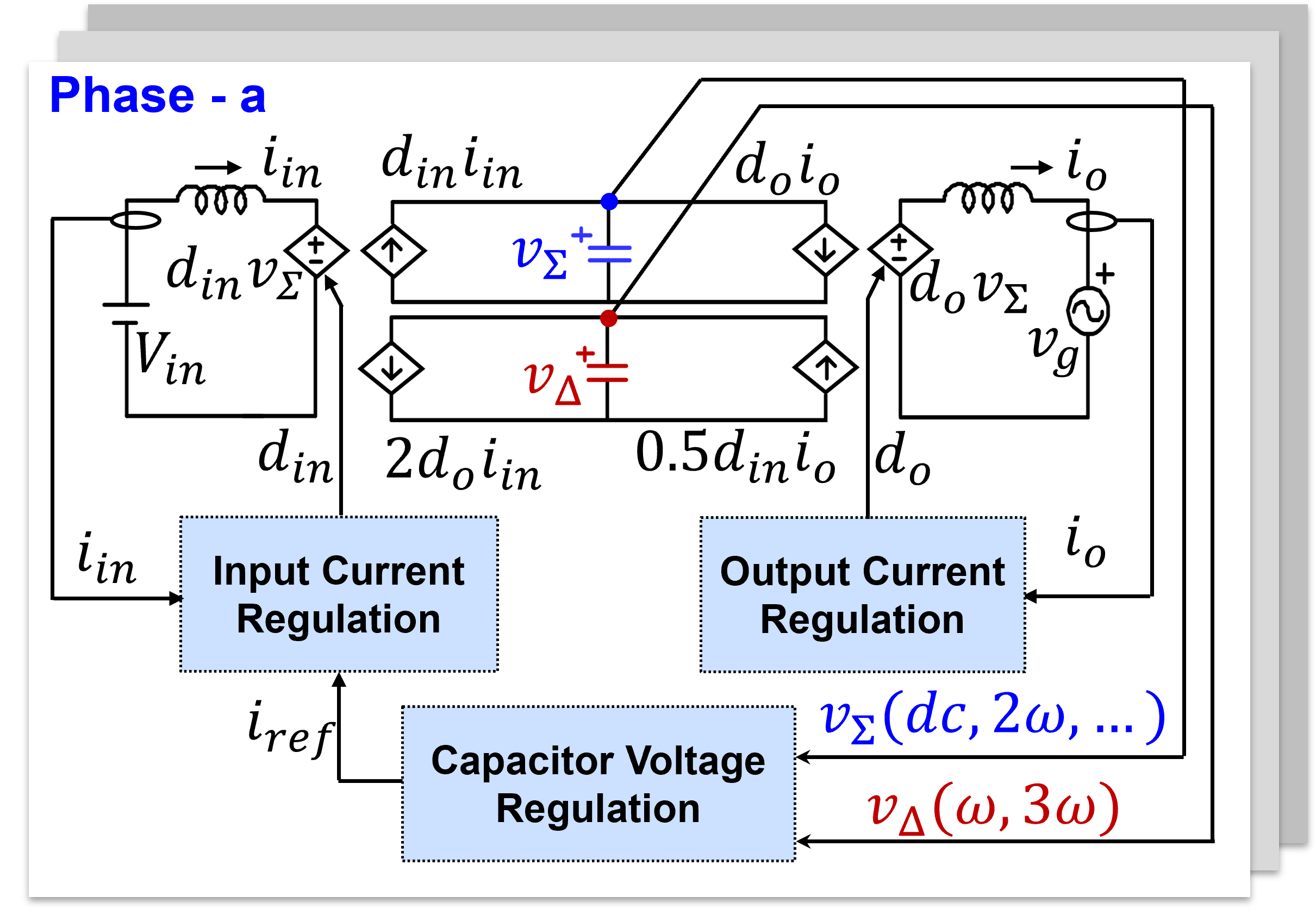
Whenever power flows from input voltage Vin to the output voltage, vg, it flows through the capacitor v∑. Thus, any imbalance between the per-phase input and output power leads to circulating energy in v∑ capacitor. On the other hand, the circulating energy related to vΔ is not associated with input or output, and therefore, merely represents the energy swapping between the upper and lower arm. These two circulating energies, related to v∑ and vΔ, are orthogonal in nature, and therefore, v∑ and vΔ are inherently decoupled to each other; v∑ has only even order harmonics while vΔ has odd order harmonics. Therefore, these capacitor voltages can be controlled independently. Moreover, the circuit model provides two ideal control laws, denoted by Eq. 1 and Eq. 2, to make the circulating energy related to v∑ and vΔ zero, respectively. Thus, the proposed circuit model clearly demonstrates two orthogonal circulating energies flowing into MMC and provides two ideal control laws as a mean to minimize them.
Apart from minimizing the circulating energies, the other control objectives in a grid-tied MMC are output current regulation, and capacitors dc voltage regulation. Conventionally, in order to achieve capacitors dc voltage regulation, the control is generally implemented in an indirect manner, in which, instead of directly controlling upper and lower arm capacitor voltages, their sum and differences are regulated. However, since sum and difference of capacitor voltages do not physically exist into the original circuit of MMC, the control implementation lacks in the physical interpretation, and rather requires rigorous mathematics. On the other hand, in the proposed circuit model, the capacitor voltages, v∑ and vΔ can be directly controlled without affecting each other owing to their orthogonal nature. It can be observed from the circuit model that v∑ and vΔ are related to current iin due to current sources, diniin and 2doiin, therefore, capacitor voltage regulation loop is tied together with input current regulation, as shown in the figure. The input current iin is regulated through din while the output current is regulated though do. Moreover, the circulating energies can be minimized by incorporating the control laws in the control implementation. For example, if the input current iin is regulated such that it can satisfy first control law i.e., iin=(doio)/din, then the circulating power related to v∑ becomes zero. Similarly, the circulating power related to vΔ can be reduced by following the second control law.
Thus, the control of MMC becomes evident under the proposed decoupled equivalent circuit model.
