LIBRARY
Input Impedance Characterization of a Single-Phase PFC in D-Q Frame
Year: 2022 | Author: Qing Lin | Paper: T-S3.5
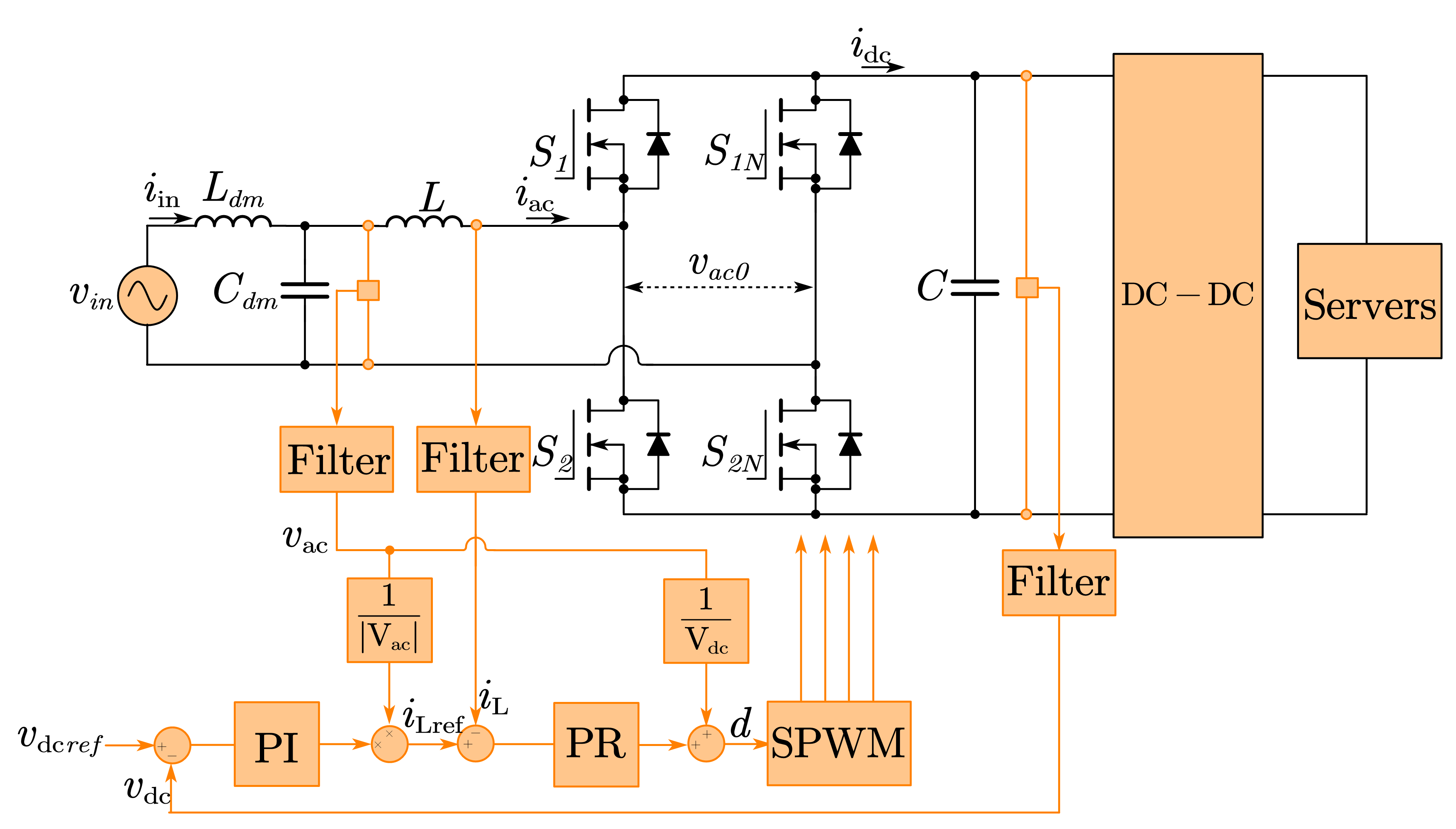
Fig. 1. Single-phase totem-pole PFC with current and voltage control
This paper studies a totem-pole topology PFC, the circuit of which is shown in Fig. 1. Its controller contains a proportional-resonant (PR) based current controller, a proportional-integral (PI) based dc voltage controller, and a phase tracking unit by scaling the input voltage by a gain of 1/|Vac|, and an ac voltage feedforward control.
Fig. 2 shows the measured impedance and the modeling results in the d-q frame in 1Hz~1kHz. The modeling results match well with the experimental results except for around 120Hz given the presence of the dc-bus double line-frequency ripples that induce the ac side third harmonics through frequency coupling, mixing the small-signal response and operating point response. The mismatch in Zdq and Zqd mainly results from the system error because the off-diagonal terms are too small. Another important point is that this mismatch is also not critical because the PFC converter impedance is diagonally dominant, and the off-diagonal terms have a negligible effect on the minor loop gain construction.
