Become a Member
Become a Member
LIBRARY
  2. Library
  3. Viewnugget
  4. 401

Inductor Geometry with Improved Energy Density

Year: 2014
Fig. 1. Ideal constant-flux inductor geometry.
The "constant-flux" concept is leveraged to achieve high magnetic-energy density, leading to inductor geometries with height significantly lower than that of conventional products. Techniques to shape the core and to distribute the winding turns to shape a desirable field profile have been devised for the two basic classes of magnetic geometries; those with the winding enclosed by the core and those with the core enclosed by the winding. A relatively constant flux distribution is advantageous not only in terms of density, but also in terms of thermal problems via the reduc-tion of hot spots, and in terms of reliability via the suppression of flux crowding. In this study of the constant-flux inductor (CFI) with enclosed winding, the foci are the operating principle, dc analysis,and basic design procedure. Prototype cores and windings are routed from powder-iron disks and copper sheets, respectively. The design of the constant-flux inductor is validated by an as-sembled inductor prototype.

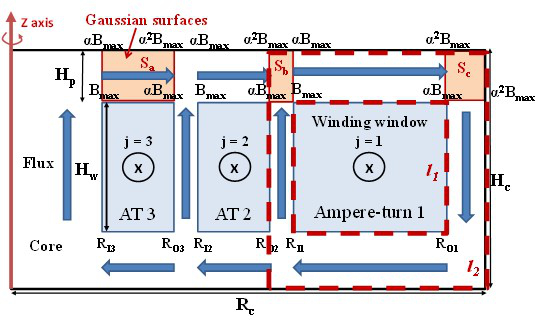
Based on the enclosed-winding geometry, the behavioral model of the constant-flux inductor can be constructed in such a way that it shapes the flux distribution and estimates the perfor-mance of the inductor. As shown in Fig. 1, an ideal constant-flux inductor with enclosed winding consists of a magnetic core with Nw winding windows carrying prescribed Ampere-turns ATj. The objective is to synthesize the Ampere-turns to constrain the flux variation to a "uniformity factor " ratio of the minimum flux density Bmax to the maximum flux density Bmax allowed in the magnetic field around winding window j. "Constant" flux is achieved when approaches unity. The model is modified to achieve a prescribed , as well as the optimal design for a constant-flux inductor.

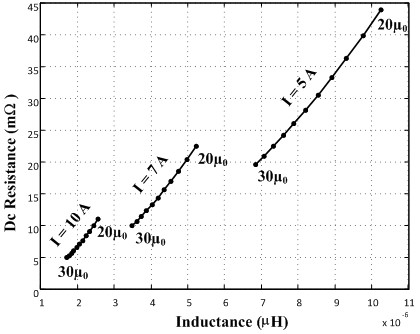
Fig. 2 gives an example of the relationships among the current rating, inductance, and dc resistance when the relative permeability changes from 20 to 30. Along each curve, the current rating is fixed while the relative permeability is swept from 20 to 30. Either a smaller permeability or a smaller current rating would increase the number of turns that each winding window represents in order to maintain the maximum flux density Bmax. By selecting the optimal variables, the performance of the inductor can be significantly improved.

Fig. 2. Relationship among inductance, dc resistance, permeability and current rating.

Our Industry Partners

About CPES

Events/Presentations

Education

Interested in Becoming a CPES Member?

Learn more


Having technical issues?

Get Help

Copyright © 2021 Virginia Tech Center for Power Electronics Systems