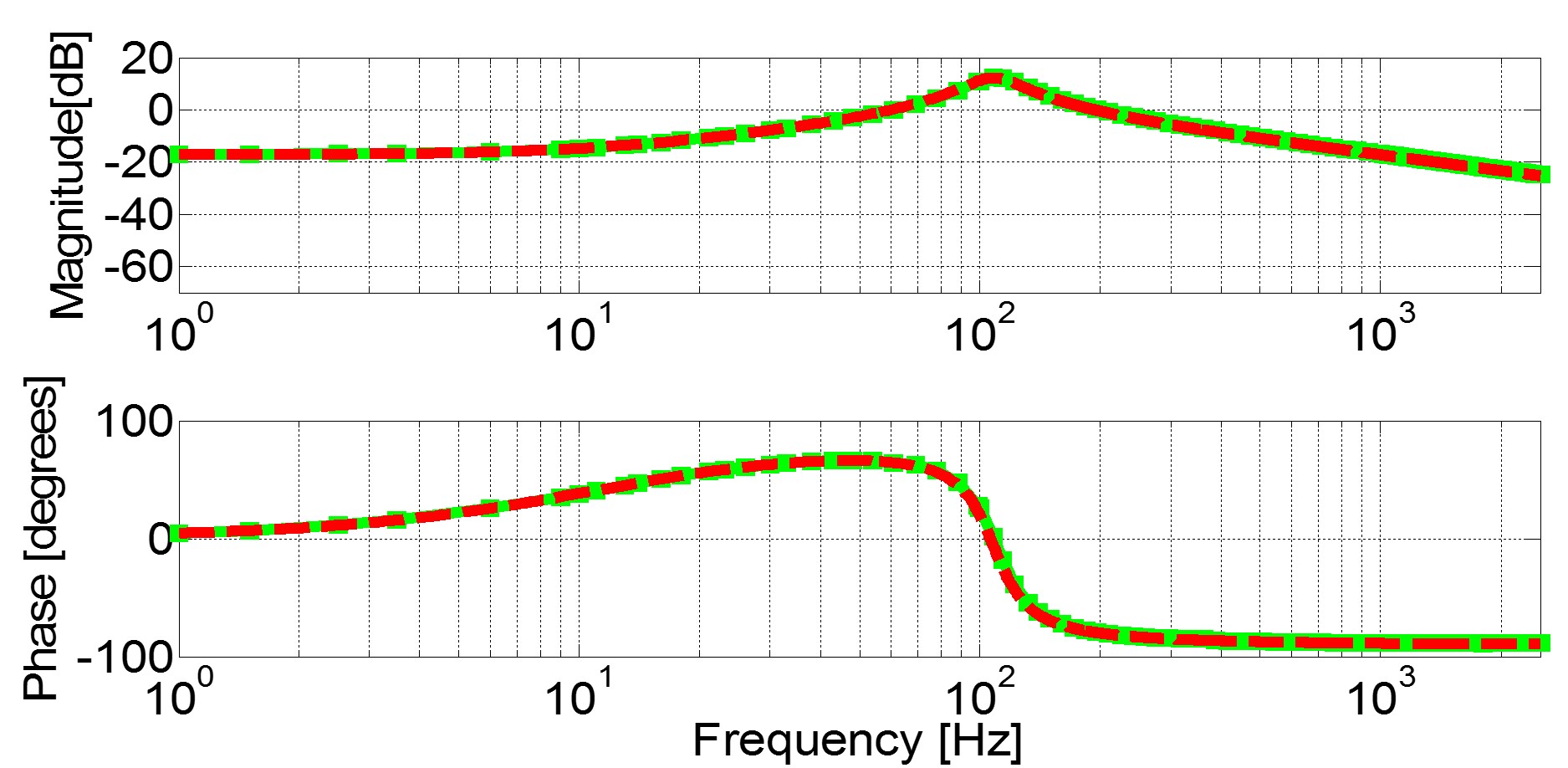
Fig. 1. (a) Small-signal input dq admittance of twelve-pulse diode rectifier: obtained from switching simulation model (green line with squares), analytical expression of modified AAVM (red dashed line)
Ydd(s).
This paper focuses on the modeling of small-signal input dq admittance of twelve-pulse diode rectifiers. It provides a comprehensive comparison of small-signal dq admittances between a well-known averaged value model (AVM), a switching simulation model and experimental measurements of a hardware set-up. Analytical AVM (AAVM) is used in the analysis since it has been commonly used to model diode rectifiers. In order to predict small-signal dq admittance accurately, the AAVM had to be modified. The modification describes injection properties in a more natural way by considering a d-channel perturbation as magnitude modulation and by considering a q-channel perturbation as phase modulation. Analytical expressions for a dq admittance of AAVM of twelve-pulse diode rectifier feeding a resistive load are derived and presented in the paper. Furthermore, it has been found that sideband admittances around multiples of switching frequency exist in the small-signal response due to the nonlinear behavior of the rectifier. The new phenomenon is analyzed theoretically, characterized in simulations with the extraction of small-signal response from the switching simulation model and captured experimentally by the hardware measurements.
Several conclusions can be drawn from the shown comparison. The first one is that AAVM predicts admittance Y
dd(s) correctly in the whole measurement frequency range, even beyond the switching frequency. The other three admittances have additional dynamics in the response that is not predicted by the averaged model. Additional dynamics are especially noticeable in admittances Y
dq(s) and Y
qq(s), as they represent response to the q-channel injection, which is more nonlinear. The additional resonant points show-up left and right around multiples of switching frequencies (720 Hz, 1440 Hz, 2160 Hz etc) and there are additional resonant points in the response at odd multiples of 360 Hz (360 Hz, 1080 Hz, 1800Hz etc). Such responses are typical for nonlinear systems, where injection at one frequency point yields several responses that are strongly coupled each to the other. The described behavior is explained with the fact that the q-channel injection modulates phase, thus it modulates commutation angle and yields significant sideband response around multiples of the switching frequency.
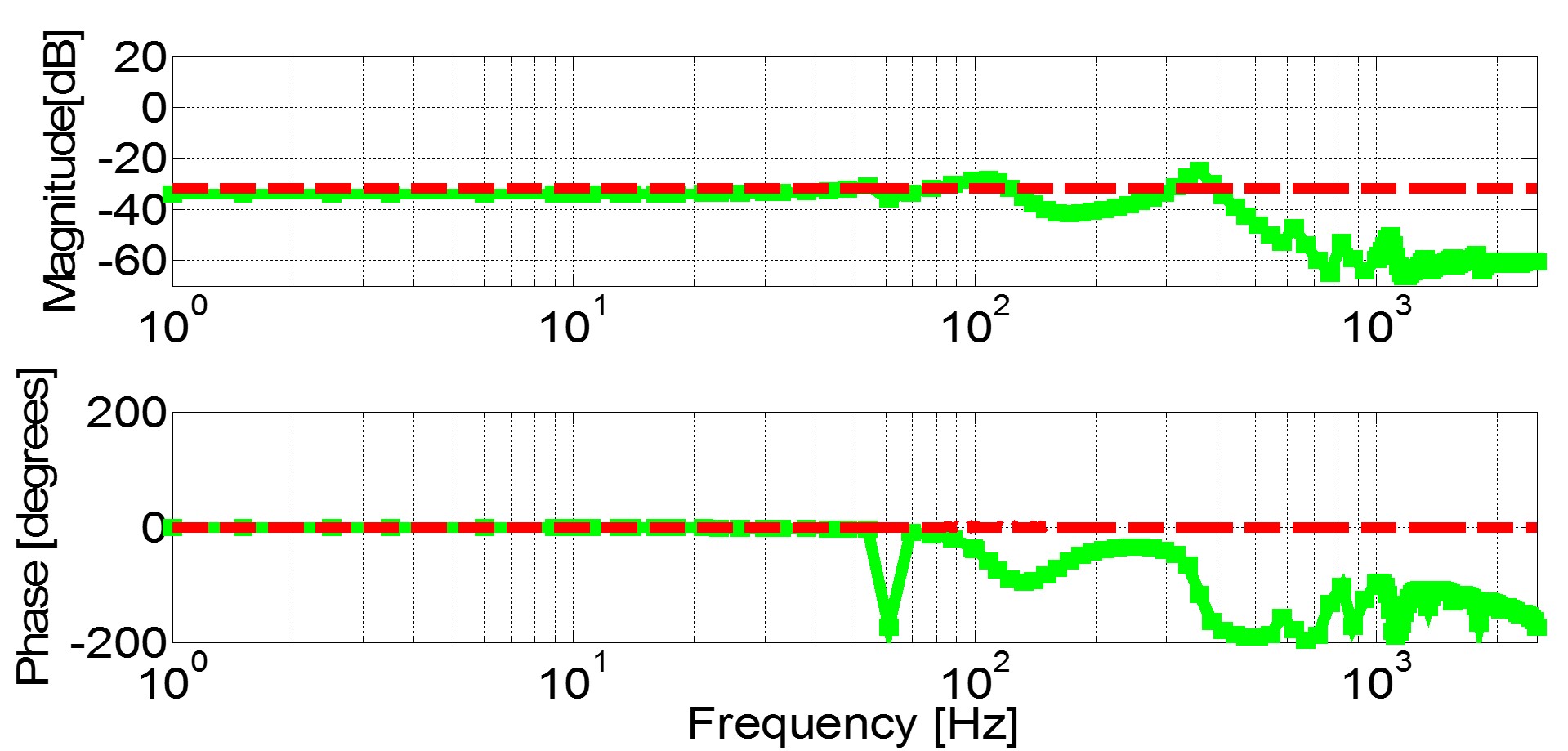
Fig. 1. (b) Ydq(s).
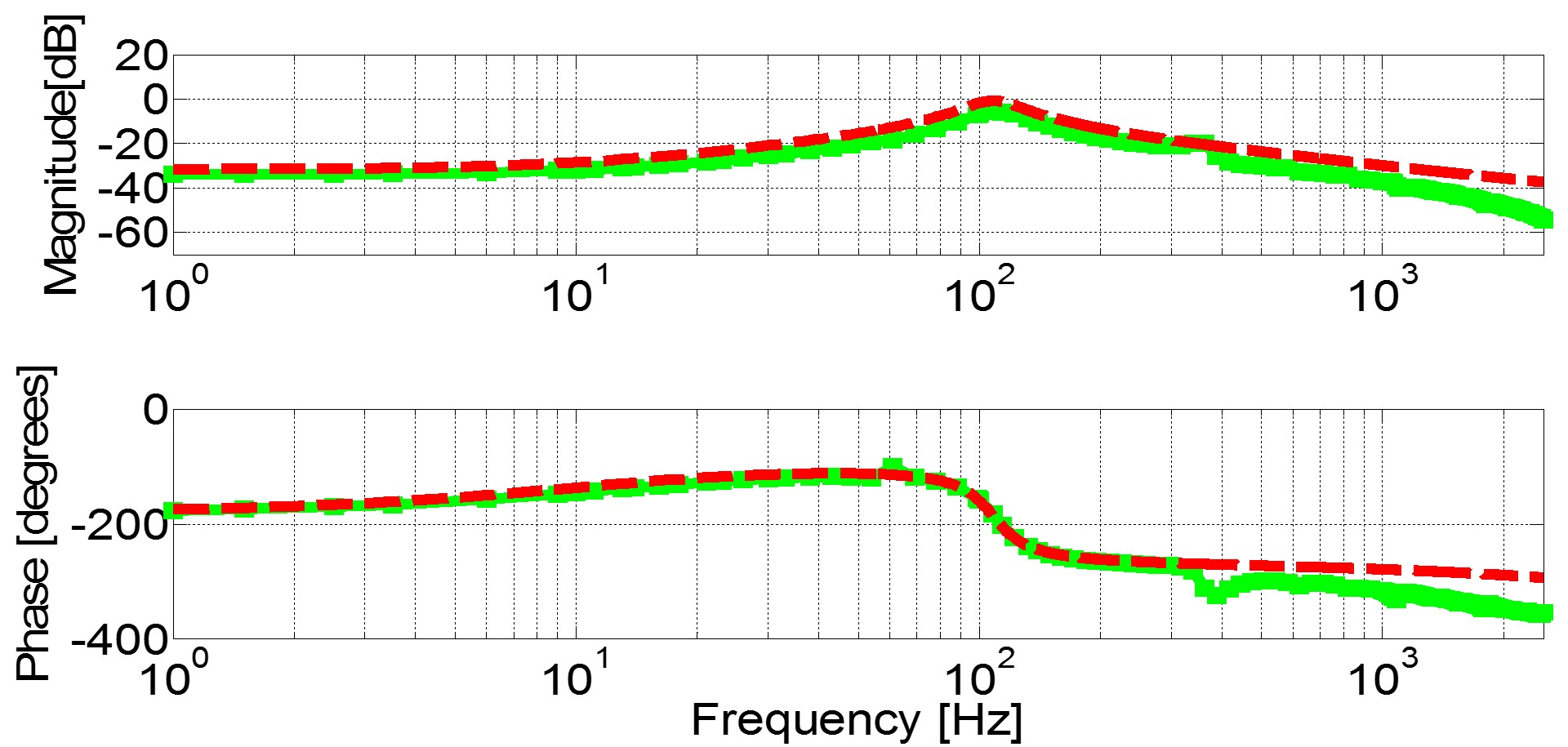
Fig. 1. (c) Yqd(s).
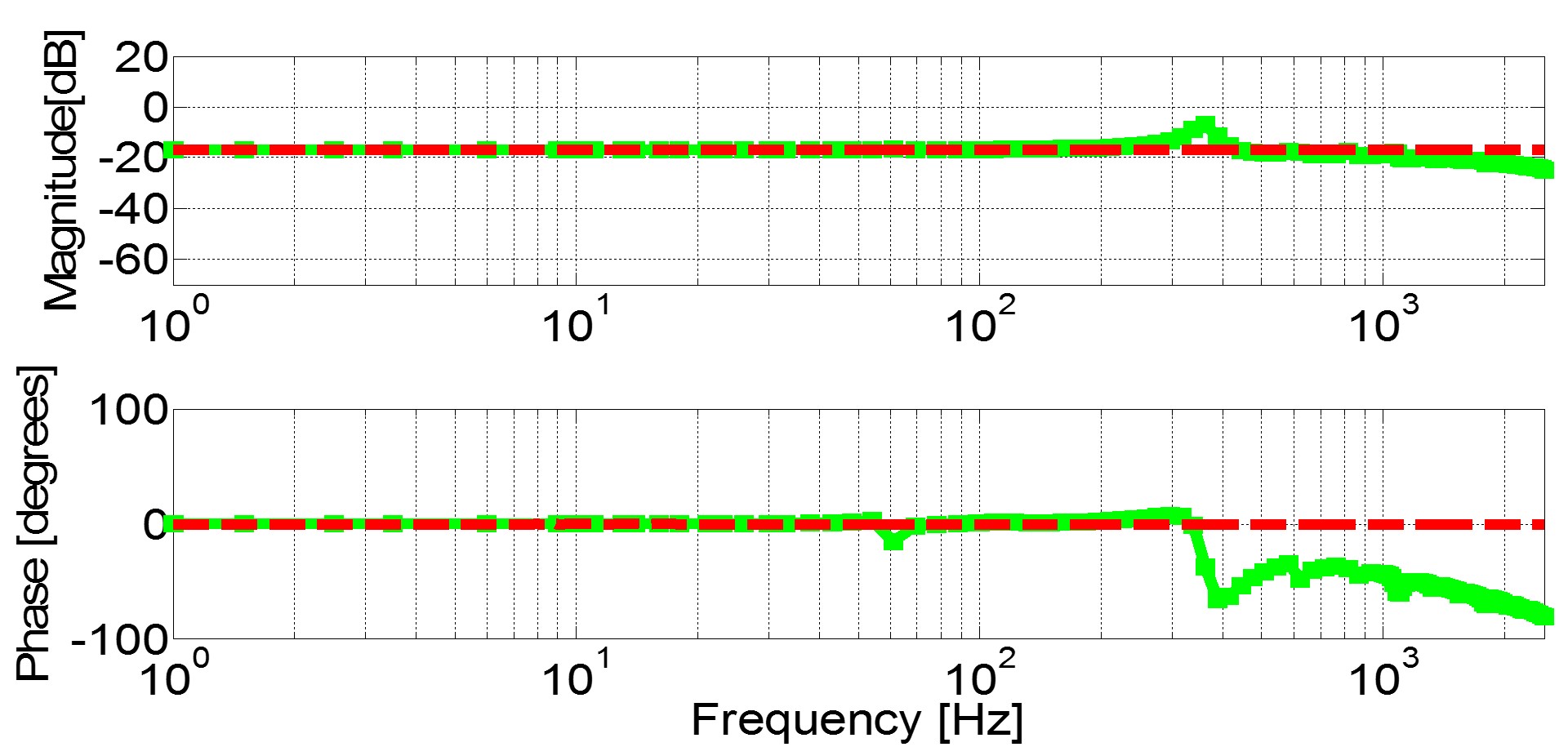
Fig. 1. (d) Yqq(s).

























































































