Become a Member
Become a Member
LIBRARY
  2. Library
  3. Viewnugget
  4. 526

Gap Design for Nonlinear Ferrite Cores to Maximize Inductance

Year: 2015
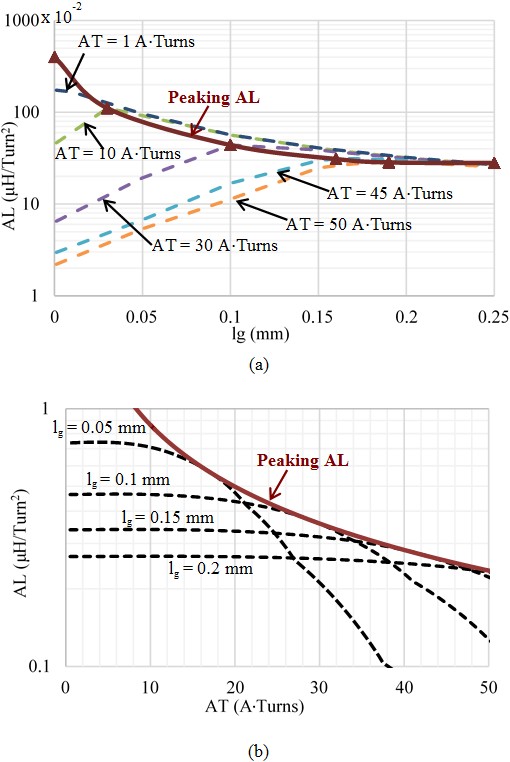
Fig. 1. (a) Simulated AL vs. gap length (lg), parametric with AT, and (b) Simulated AL vs. AT, parametric with lg.
This paper demonstrates that in the presence of nonlinearity, inductive energy may be partially stored in the core, leading to a higher inductance. The objective is to find the optimal gap length to store the highest energy and reach the maximum inductance for a given dc current. Fig. 1(a) illustrates simulated inductance versus gap length, parametric with dc (bias) ampere-turns AT. When dc current is high, e.g., 30 ATurns, there is one peak point on each curve. The maximum points of each curve constitute the line "Peaking AL" plotted as the solid line Fig. 1(a), which can also be plotted in the graph of AL versus AT, parametric with gap length in Fig. 1(b). For a fixed gap length, AL decreases with AT and is tangential to the curve of peaking AL. If the objective is to improve the inductance at heavy load, the "peaking AL" should be employed. The design for the swinging inductor needs a series of curves of AL versus AT plotted as dash lines in Fig. 1 (b).

From the specified L and I, the load curve AL = LI2 / AT2 is plotted as the dotted curve in Fig. 2 (a). The load curve intersects the curves of maximum AL at the solution points P1, P2, and P3. Those points determine operation points for maximum inductance. From the specified non-linear inductance, the heavy-load curve AL = LminImax2/AT2 and light-load curve AL = Lmax1Imin2/AT2 are also plotted in Fig. 2 (b). Not all the intersection points are valid to determine effective operating statuses. Valid intersection points should satisfy ATmax/ATmin = Imax/Imin. The only solution is the pair (M4,M3) since AT@M3/AT@M4 = 50/10 = Imax/Imin. Both gap length and intersection points should be correct to determine the operating AT.

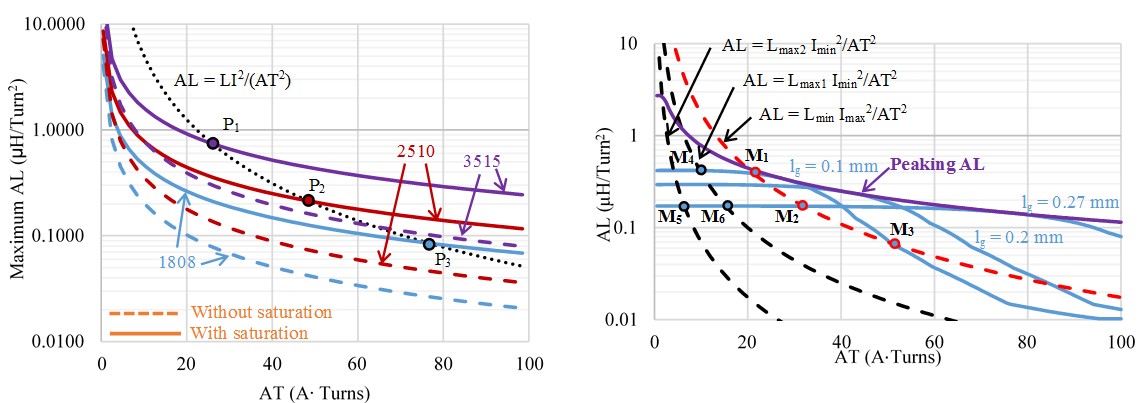
Fig. 2. (a) Maximum AL vs. AT calculated by conventional model without saturation and by model with saturation for core size 2510 and P-ferrite, intersecting AL = LI2/AT2 for L = 5 uH and I = 5 A. (b) Modeled AL vs. AT, parametric with gap length (lg) for core size 2510 and P-ferrite, intersecting AL = LI2/AT2 for Lmax1 = 40 uH, Lmax2 = 7 uH, Lmin = 7 uH, Imin = 1 A, and Imax = 5 A.

Our Industry Partners

About CPES

Events/Presentations

Education

Interested in Becoming a CPES Member?

Learn more


Having technical issues?

Get Help

Copyright © 2021 Virginia Tech Center for Power Electronics Systems