LIBRARY
Synergetic Optimization of Efficiency and Stray Magnetic Field for Planar Coils in Inductive Power Transfer Using Matrix Calculation
Year: 2017 | Author: Ming Lu | Paper: D1.6
Fig. 1. Planar coil with ferrite plate in IPT.
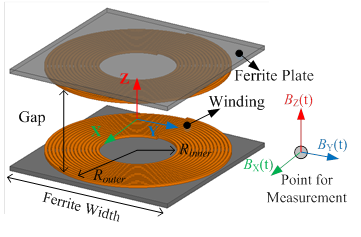
Efficiency and stray magnetic fields are influenced simultaneously by design of coils' pa-rameters, such as inner radii, outer radii, and distribution of turns. Their synergetic optimization is important. Pareto front of coils' efficiency versus a stray magnetic field is suitable for this kind of multi-objective optimization. Physical parameters are swept in finite-element simulation (FES) to derive the Pareto front. However, the problem of a parametric sweep is that it asks for thou-sands of simulations that are time-consuming especially for 3D simulation.
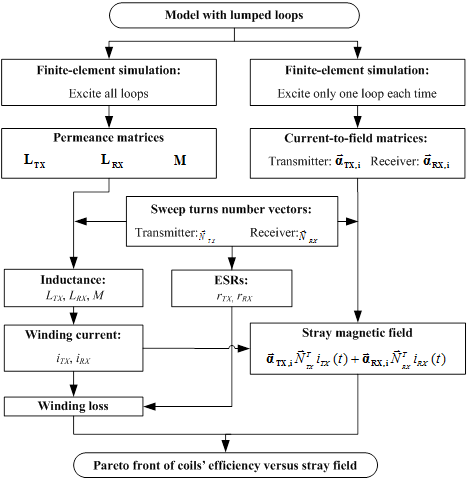
A faster method using matrix calculations is demonstrated in this paper. Efficiency and magnetic field are calculated with winding vectors, permeance matrices, and current-to-field (I-B) matrices instead of being simulated. Physical parameters of coils including inner radii, outer radii, and distribution of turns are represented with winding vectors. The parametric sweep in simula-tion is replaced by sweeping winding vectors in matrix calculation to derive Pareto fronts for op-timization. Only tens of simulations are required in the optimization procedure using the matrix calculation. Fig. 2 shows the optimization procedure.
Accuracy of the matrix calculation is verified by comparing with experimental measurement for a set of exemplary coils. The maximum difference of the exemplary coils between calculation and measurement is 4% for inductances, 9% for ESRs, and 12.5% for stray magnetic field.
Fig. 2. Flowchart of synergetic optimization of coils' efficiency and stray magnetic field for IPT coils.
