LIBRARY
Dynamic Interactions in Hybrid AC/DC Electronic Power Distribution Systems
Year: 2012
Fig. 1. DC subsystem under test.
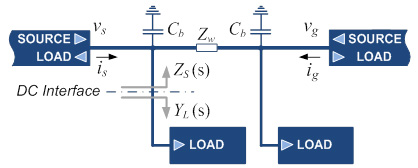
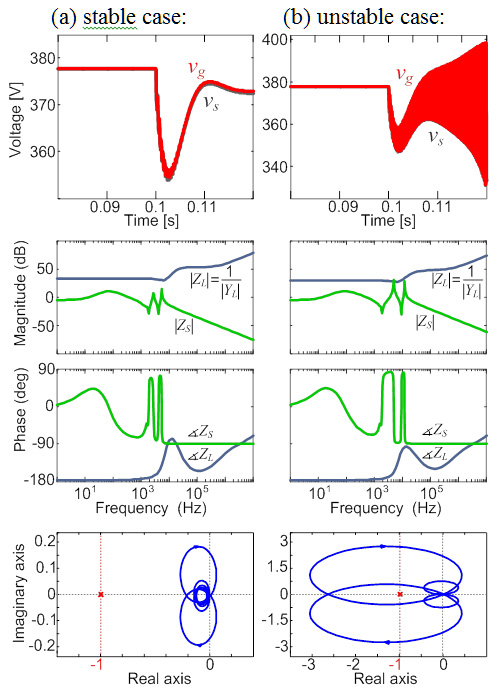
The unstable operation of the power distribution sub-system depicted in Fig. 1 occurs as a result of insufficient bus capacitance Cb. Fig. 2 shows the time domain responses in both stable and unstable cases.
The Bode plots of the impedances at the DC interface (shown in Fig. 2) were obtained using small-signal analysis with the average model of the system, shown in Fig. 1. The load input impedance clearly shows the CPL characteristic up to a few kilohertz (∠ZL ≈ '180°). Under the stable case shown in the Bode plots in Fig. 2a, the magnitude of ZS is lower than ZL with a sufficient margin, while in the case shown in Fig. 2b, an equivalent source impedance resonant peak interacts with ZL, leading to unstable operation after the sudden load step at 0.1 s. The stability of the system in Fig. 1 highly depends on the return ratio,
L(s) = Zs(s) YL(s) (1)
which for the stable systems must not encircle point -1. Nyquist diagrams for both stable and unstable case are shown in Fig. 2.
Similarly, for the arbitrary ac system, the loci of the eigenvalues of return ratio L(s) (shown in (2)), as specified in the generalized Nyquist stability criterion (GNC), must not encircle the -1 point.
The paper provides examples of dynamic interaction, and raises possibility of addressing stability by employing terminal-behavioral modeling.
Fig. 2. Time-domain, frequency response waveforms and Nyquist diagrams of the return ratio for (a) stable, and (b) unstable cases at the DC Interface in Fig. 1.
